


◆ 伝送では、回線使用率が高くなると、輻輳のために、送信要求が発生しても、直ちに送信できない場合があります。電話のお話中に相当する現象です(図.33)。
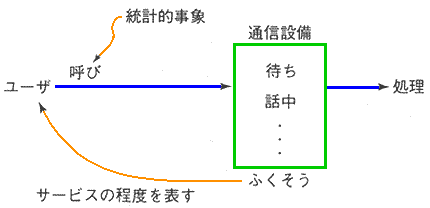
◆ 電話の場合には、お話中のときは、一旦切って、改めてダイヤルします。
しかし、データ伝送の場合には、伝送要求を出したとき、お話中であっても、そのまま、待ち続けて、空いたら送信を行う方式が存在します。
◆ 何れの場合であっても、待ちの状態を、定量的に評価することが必要です。通信システムにおける待ち時間の解析を、トラフィック解析 と呼んでいます。そして、トラフィック解析のバックグラウンドとなる理論が、トラフィック理論 です。
◆ たとえば、電話の交換機を考えます。交換機の容量が大きければ、お話中は少ないでしょう。その代わり交換機が高くなり、最終的には電話料金が高くなるでしょう。したがって、この兼ね合いが重要です。トラフィック理論は、この問題を定量的に解析する手段です(図.34)。
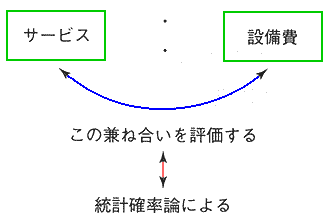
◆ トラフィックは、確率現象です。したがってトラフィック理論は、統計確率をベースにしています。
◆ トラフィック解析は、通信システム全般に適用されます。待ちが発生するシステムであれば、通信以外にも適用可能です。しかし、具体的な挙動は、システムによってかなり異なります。
ここでは、具体的な対象として、LAN を取り上げます。なお、比較の対象として電話網を取り上げて解説します。したがって、かなり一般的な内容になっていますから、LAN 以外の対象にも役立ちます。
◆ トラフィック解析は、その対象範囲によっても、大きく異なります。待ちの発生場所が、あちこちにあるからです。LAN システムにおける、待ちの発生個所を、図.35 に示します。
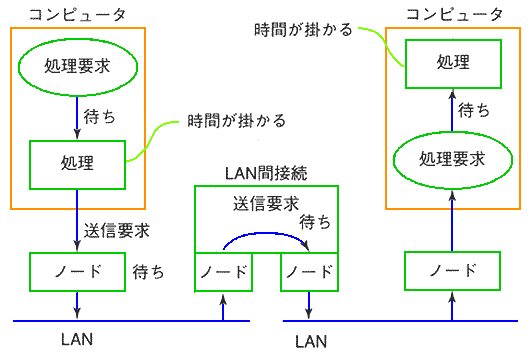
◆ 図に示したように、待ち以外の処理時間もあります。しかし、以降で解説するのは、LAN 単体です。
◆ トラフィック理論は、電話交換機を対象に発展しました。LAN でもこれを利用します。交換機を抽象化したモデルを考えます。これを交換線群 といいます(図.36)。
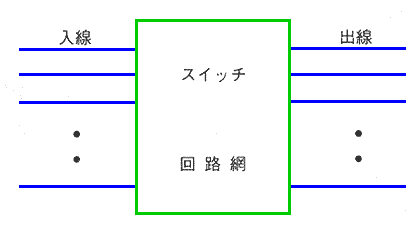
◆ 入線 に発生した呼びは、接続可能であれば、空きの出線 の 1 本に接続されます。接続不能の場合は、予め決められた方法で処理されます。電話の場合には、お話中となり受け付けられません。これを損失 といいます。このような接続のやり方を、即時式交換線群 といいます(図.37)。

◆ LAN の場合には、損失にはならないで、接続可能になるまで、待ち合わせ、出線が空いたら接続します。この方式を、待時式交換線群 と呼びます。LAN は、共用伝送路ですから、出線は 1 本です(図.38)。
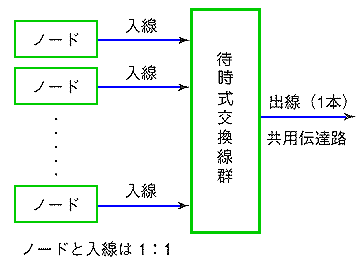
◆ 通信の用語で、繋がってる状態、すなわち、使用している状態を、保留 と言います。1 本の入線または出線に、同時に 2 つ以上の呼びが保留されることはありません。
交換線群には、完全線群 と不完全線群 の 2 種類があります(図.39)
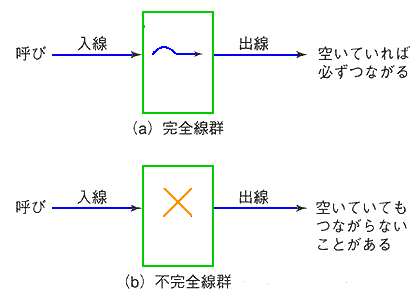
◆ LAN は完全線群と考えられます。
◆ 交換線群において、呼びが回線を、どのように占有するかは、呼びの生起や、復旧の確率分布によって決まります。復旧 も通信の用語で、呼びが切れることを言います。
図.40 の(a)は、電話における、呼びの保留状態を示したものです。各横線は入線または出線をあらわし、太線は呼びによって回線が保留されている時間を示します。
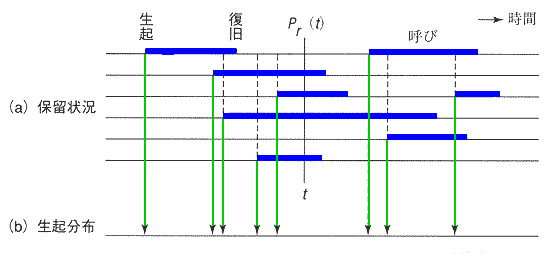
◆ 図の(b)は、呼びの生起時点だけを示したもので、呼びの生起分布 を表わします。呼びの生起分布は、呼びの発生源の統計的性質から決まります。また、呼びの継続時間、すなわち保留時間分布は、呼び自体の性質から決まります。
◆ 公衆電話網における呼びの生起は、1 日の時間帯によって大きく変動します(図.41)
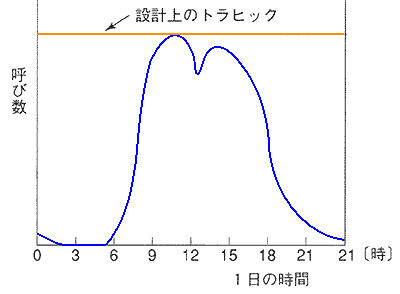
◆ この図は、単位時間あたりの平均呼び数を表わしています。実際には、瞬間的に見ると、細かく変動しています。
1 日 24 時間のうち、ピークとなる 1 時間を、最繁時呼び数 といいます。また、1 日の総呼び数に対する最繁時呼び数の割合を最繁時集中率 といいます。公衆電話網の場合には、10 〜 20% 程度です。トラフィック解析では、この最繁時呼び数を使って、設計を行います。
◆ しかし、LAN では、個々のシステムによる違いが大きく、一概には言えません。公衆電話網に比べると、はるかに規模が小さいので、顕著なピークが存在します。最繁時間も、1 時間よりも、はるかに短い時間で考える必要があります。
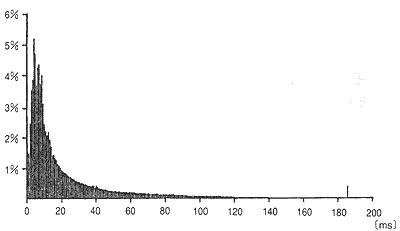
◆ 図.42 は、あるイーサーネットの呼び量を実測した例です。呼び数ではありませんが、傾向は同じです(呼び量は次に示します)。
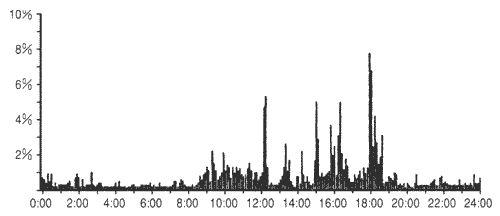
◆ この図は、6 分間の平均負荷を取ったものです。しかし、さらに、この中の、特定の 4 分間について調べると、図.43 のようになります。
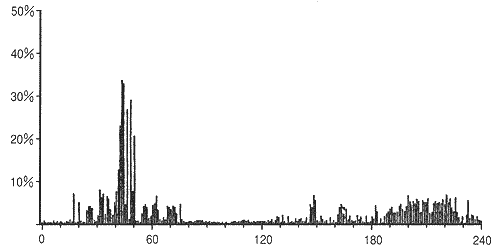
◆ 図.42 では分からなかった、顕著なピークがあります。LAN の伝送速度が、これを賄い切れなくても、CSMA でなければ、待ち時間が増加するだけです。しかし、CSMA では、渋滞になる可能性があります。
◆ 以上から、LAN の伝送速度を決めるときには、呼びの分布を推定しておくことが、重要です。しかし、LAN では、個々のシステムによって、大幅に異なります。そして、予め推定することが困難なことも多いのです。
LAN のトラフィック量は、日時と共に増加します。この将来の増加分を見込んで、十分に余裕を取っておくことが、実用的です。
◆ トラフィック量 は、回線の延べ保留時間で定義されます。しかし、呼び量 で評価する方が、より適切です(図.44)。
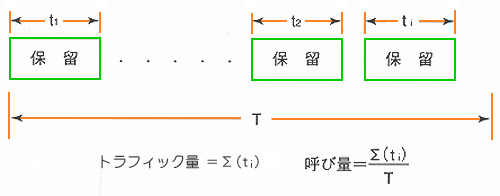
◆ トラフィック量は、時間によって変動します。これを単位時間あたりに換算した量が、呼び量です。この呼び量のことを、トラフィック密度 とも言います。
時間区間 (t,t+τ) 内のトラフィック量を T(t,τ) としたとき、その間の呼び量を A(t,τ) とすれば、
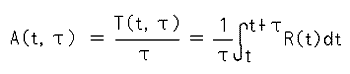
で表わされます。ただし、R(t) は、時刻 t において、回線を保留している呼びの同時接続数です。
◆ τ→ 0 で、A(t,τ) の極限が存在するとき、その値を、その時刻 t における瞬間呼び量 といいます。
τ→ ∞ の A(t,τ) の値を平均呼び量 といいます。ランダムかつ定常的な場合は、瞬間呼び量と一致しますから、両者を区別する必要はありません。
◆ 平均呼び量は、次のようにも表わされます。
a = λ h
ただし、λ は単位時間あたりの平均呼び数、h は平均保留時間です。
この平均呼び量は、無次元数です。しかし、これに単位をつけて、アーラン と呼び、erl と略記します。
◆ トラフィック理論で、最も基本的な交換線群は、完全線群です。LAN も完全線群です。
完全線群の特性は、呼びの生起分布、保留時間分布、待ち合わせ呼びの性質、交換処理の方法などによって定まります。これらの特性を決める条件を、ケンドール記号と呼ばれる記号で表現します。
◆ ケンドール記号は、
X / Y / n (m,ξ)
の形で表わします。
第 1 記号 X は、呼びの生起条件を表わし、生起間隔の確率分布の形で表わします。
第 2 記号 Y は、保留時間の確率分布です。
第 3 記号 n は、出線の数を示します。
第 4 記号は ( ) の中で、m は、待ち合わせ許容呼び数です。即時交換線群では、m = 0 です。LAN では、m ≠ 0 です。
ξ は、ξ = h / τ で、h は平均保留時間です。τ は、待ち合わせ呼びが、どのくらい我慢して待つかを示す時間で、平均待ち合わせ滞留時間 といいます。
◆ 通信で多く出てくる確率分布系を、紹介しておきます。
指数分布 : 通信における最も一般的な分布です。指数分布のケンドール記号は、M です。通信以外の一般的現象では、ランダムなのもが正規分布になリます。通信ではランダムな現象は、指数分布になります(図.45)。
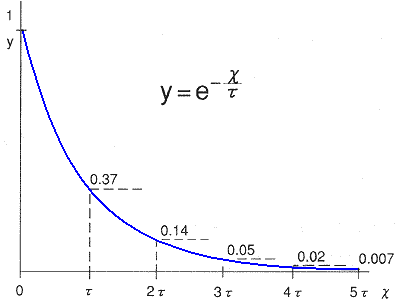
◆ たとえば、呼びの生起分布は一般に指数分布になります。LAN でも指数分布です(図.46)。
◆ 保留時間分布は、指数分布とは見なせないことも多いのですが、指数分布は数学的な取り扱いが簡単なので、指数分で近似します。
一定分布 : 値が一定の分布です。一定分布のケンドール記号は、D です。保留時間分布では、一定分布とみなせるものがあります。
通常の LAN では、パケット長さは、決められた最大長さの範囲で可変です。しかし、ネットワーク伝送では、パケット長さが固定のものもあります。この場合は一定分布です。
◆ 一般分布 : 指数分布、一定分布の何れにも属さない分布形のものを、ひっくるめて、一般分布と呼んでいます。ケンドール記号は、G です。
◆ LAN の呼びの生起分布は、前述のように、一般に指数分布になります。しかし、保留分布は様々です。
可変長パケットのシステムにおいても、パケット長さは、最小長さと、最大長さとがあります。長いメッセージを送るときは、最大長さのパケットに分割して送ります。また、ユーザーデータの他に、制御パケットのやり取りがあります。制御パケットは、一般に最小長さのパケットです。
◆ 以上から、パケット長さは、最小長さと、最大長さのものが多くなります。パケット長さの分布の一例を、図.47 に示します。
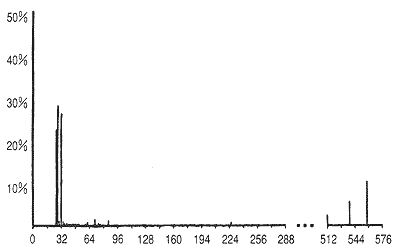
◆ LAN のパケット長さの分布は、以上に示したとおりですが、実用上は、次の 2 種類で、近似します。
M / M/ 1 (∞ , 0) : 呼びの生起分布と保留時間分布が、共に指数分布です。LAN の出線の数は 1 ですから、第 3 記号は 1 です。第 4 記号の ∞ は、待ち合わせ許容数が無限大ということです。
◆ 実際には、バッファ長さで制約されます。その結果として、バッファオーバーフローで廃棄されるパケットが発生します。しかし、これを無視します。
第 4 記号の最後の 0 は、待ち合わせ滞留時間が無限大であることを意味します。一般にLAN のノードでは、ユーザーから取り消されない限り、いつまでも待ちます。ユーザーのタイムアウト処理によって、取り消されますが、タイムアウト処理は、異常処理です。
◆ M / D / 1 (∞ , 0 ) : これは、固定長パケットです。したがって、保留時間分布が一定分布になります。その他は、M/M/1(∞,0) と同じです。
◆ 待ち合わせシステムでは、窓口を多数で共用した方が、待ち時間が短くなります。これを、大群化による能率向上といいます。この原理を活用して、昔と今とでは、行列の作り方が改善されています(図.48)。
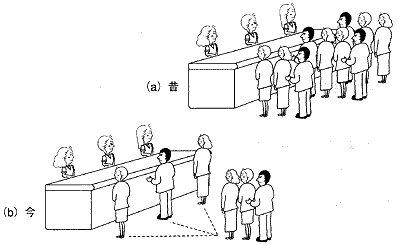
◆ 通信システムにおける窓口の数は、出線の数です。
交換線群の出線が、時間的に使用されている割合を、出線の使用率 といいます。これを η とし、a を入線から加えられる呼び量、B を呼び損率(お話中の確率)、n を出線の本数とすれば、即時式完全線群(電話)においては、
η = a ( 1 - B ) / n
となります(図.49)
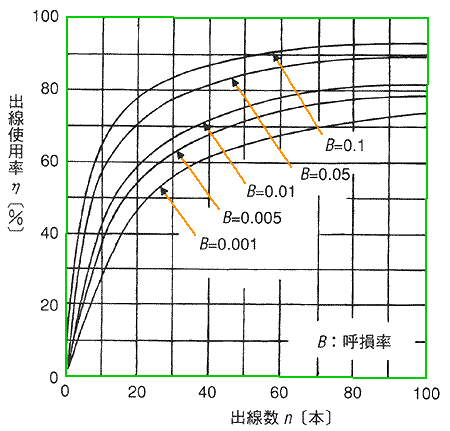
◆ この図から、次のことが分かります。
呼び損率 : 呼び損率を大きくすれば、出線の使用率が向上します。すなわち、サービスを犠牲にすれば、装置が安くなります。
出線の数 : 出線の数が多いほど出線の使用率が高くなります。すなわち、大群化による能率の向上です。
◆ LAN は待時式完全線群です。LAN は、出線の数が 1 ですから、大群による能率の向上を見込むことはできません。
しかし、LAN は、タイムシェアリング的に動作します。パケット単位で考えると、大群による能率の向上は、ありませんが、メッセージ単位で考えると、大群化による能率の向上を期待することができます。