


◆ 負荷があるときの応答は、追値制御で検討します。
目標値のパターンは、いろいろありますが、代表的な2種類について示します(台形制御もこの2種類の組み合わせです)。
追値制御では、図 6-2-33 に示したようなリミットに、引っ掛からない条件で制御する必要があります。その条件でシミュレートします。
[注] モータ単体についても、ここの図の方が、詳細な応答が分かります。
◆ モータに、減衰の無い慣性モーメントだけの負荷を掛けたときを検討します。
◆ 起動時に、一定速度で立ち上げるときの応答を、図 6-2-34〜図 6-2-38に示します。
[図 6-2-34] 減衰が無い負荷(立ち上がり)(回転角度)
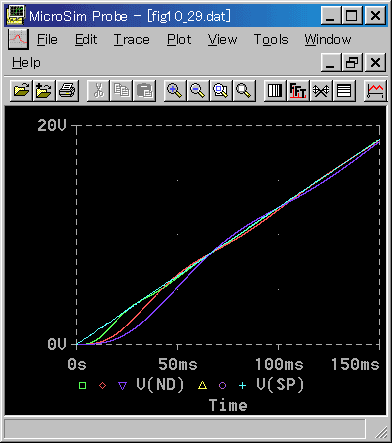
[図 6-2-35] 減衰が無い負荷(立ち上がり)(偏差)
◆ 回転角度の応答を、拡大して見るために、偏差をとったものです。
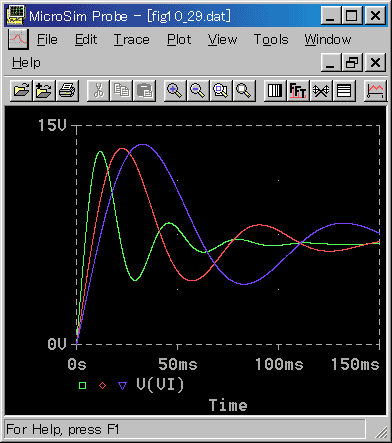
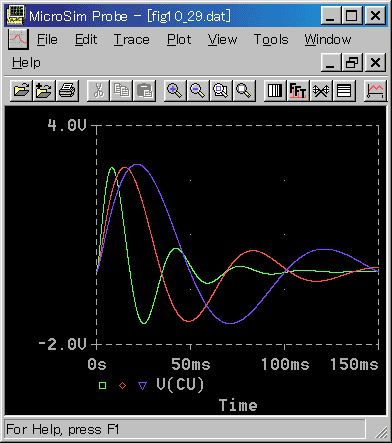
[図 6-2-38] 減衰が無い負荷(立ち上がり)(回転速度)
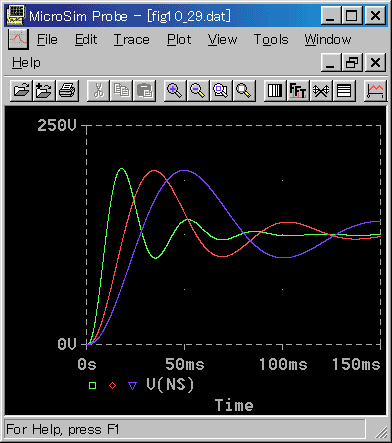
◆ 制御パラメータは、それぞれ調整してあります。順に、KP=13 TI=30ms、KP=7 TI=50ms、KP=5 TI=70msです。速度制御のときと異なり、負荷が大きくなると応答が遅くなります。
一定速度の立ち上げですから、結果的に一定速度の制御を行なっています。
速度制御だけを行なうのであれば、6.2.1.(3)に示した速度制御の方が、まともですし、制御応答も高速です。
しかし、アクチュエータや、ロボットの制御では、各種の制御を行ないます。
応答速度が問題にならないときは、位置の追値制御の一部として、速度制御を行なうことも、多く行われています。
◆ 一定速度で動いているとき、これを停止するときの応答を図 6-2-39〜図 6-2-42に示します。
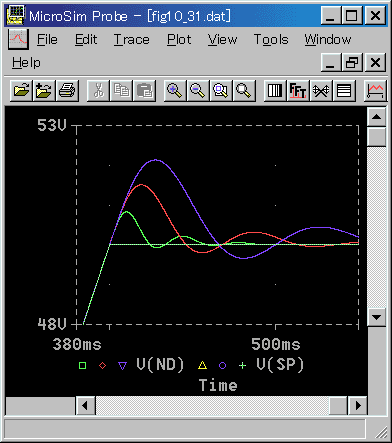
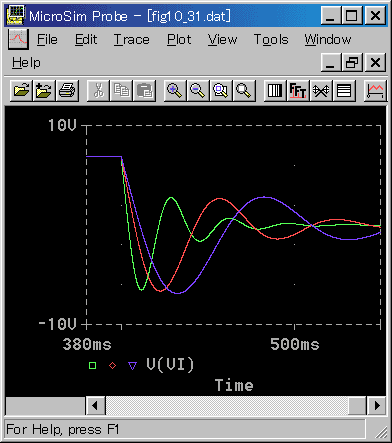
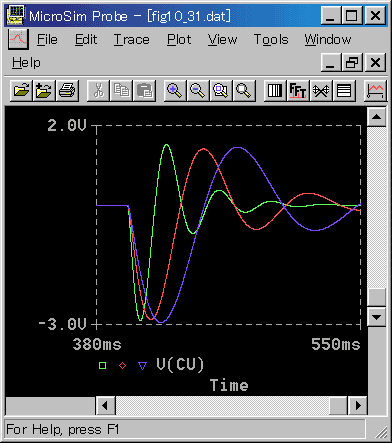
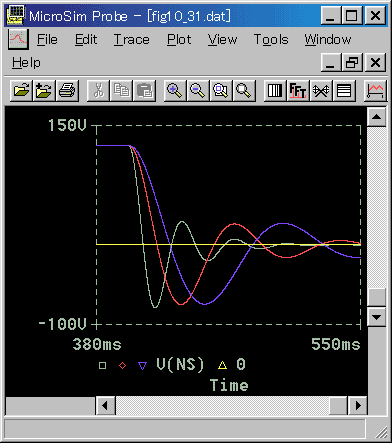
応答は、立ち上がりと大体同じです。
◆ 位置の定常状態は、モータの停止ですから、電圧、電流、回連速度の定常値は、すべてゼロです。
慣性モーメントがモータと等しく、減衰のある負荷を接続したときの応答を示します。減衰定数DNは順に、0、0.001、0.002です。
◆ 起動時の立ち上がりの応答を、図 6-2-43〜図 6-2-47 に示します。
[図 6-2-43] 減衰が有る負荷(立ち上がり)(回転角度)
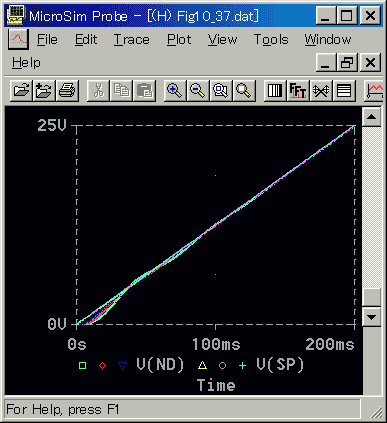
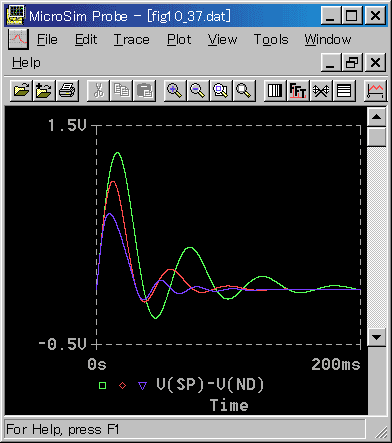
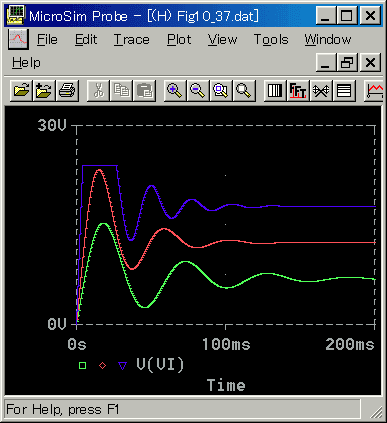
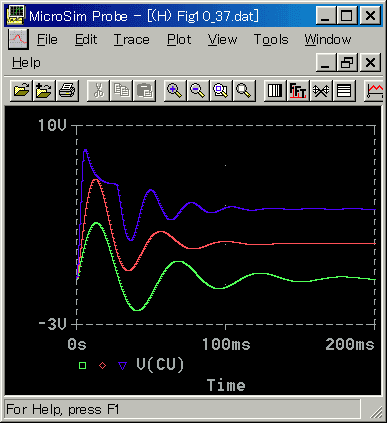
[図 6-2-47] 減衰が有る負荷(立ち上がり)(回転速度)
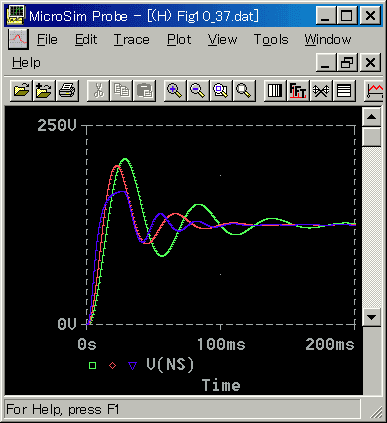
◆ 減衰が大きいほど応答が速くなります。制御パラメータは、それに合わせて調整してあります。
順に、減衰無し(DN=0) KP=10 TI=50ms、DN=0.001 KP=18 TI=30ms、DN=0.002 KP=45 TI=20msです。
図 6-2-45 をみると、DN=0.002は、電圧のピーク時に、リミットに達していることが分かります。これが原因にになって、リミットに掛からなかったときに比べれば、応答速度は遅くなっているはずです。
しかし、DN=0.001に比べれば、速くなっています。一時的にリミットにかかったときは、この程度で済みます。
リミッタを外したときとの比較を、図 6-2-48 に示します。
[図 6-2-48] リミッタ無しとの比較(偏差、電圧)
とは言っても、やはり、この程度は違います。
◆ 停止時の応答を示します(図 6-2-49〜図 6-2-52)。
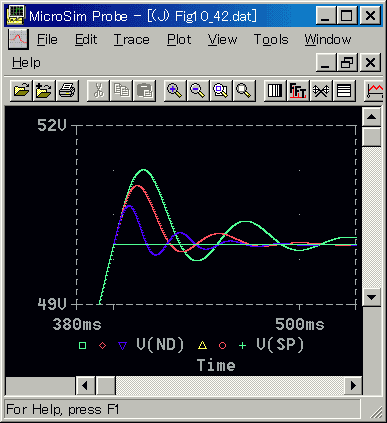
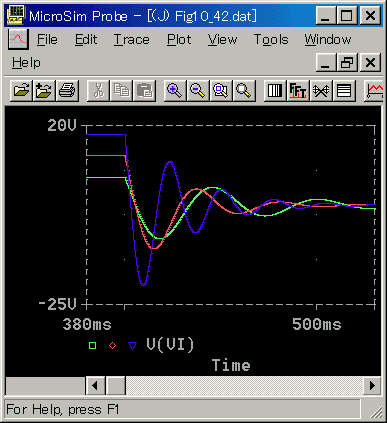
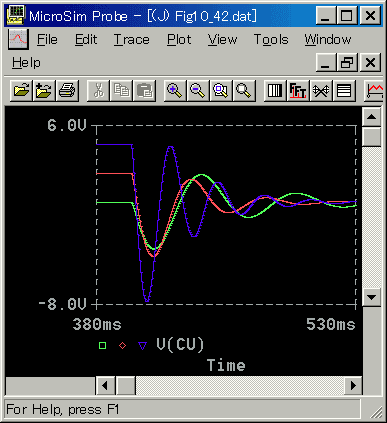
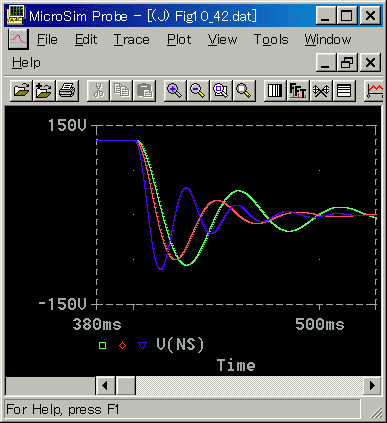
◆ 起動時と、ほぼ同様です。電圧等が最初に水平になっている部分は、位置が一定速度で変化しているときの、状態です。
なお、停止時には、電圧のリミットに掛かりませんから、減衰定数DN=0.002のものは、リミットによる応答の遅れはありません。この点が、起動時とは異なります。